Matematica Semplice

Matematica Online per tutti

Come Calcolare un’Espressione Numerica

In questa guida spieghiamo come calcolare un’espressione numerica.

Le seguenti espressioni A, B, C e D si chiamano espressioni numeriche
A = (9 – 3) x 2 + 1
B = 9 – 3 x 2 + 1
C = 9 – (3 x 2 + 1)
D = 9 – 3 x (2 + 1)
Pur avendo gli stessi numeri e gli stessi simboli delle operazioni, non si calcolano tutte allo stesso modo e, per ognuna, si ottiene un risultato differente:
(A = 13; B = 4; C = 2; D = 0).
Vediamo quali risultano essere le regole da seguire per calcolare queste espressioni.

Sequenza delle operazioni

Per calcolare un’espressione numerica scritta senza parentesi, si eseguono i calcoli da sinistra verso destra, cominciando sempre dalle moltiplicazioni e dalle divisioni, che devono essere svolte prima delle addizioni e delle sottrazioni.
Nota: Se in un’espressione compaiono solo addizioni e sottrazioni (oppure solo moltiplicazioni e divisioni), si effettuano tutti i calcoli in ordine, da sinistra verso destra.

Esempio: B = 9 – 3 x 2 + 1.
Prima di tutto risolviamo la moltiplicazione, che ha la precedenza rispetto all’addizione e alla sottrazione:
B = 9 – 6 + 1.
Si esegue quindi la prima operazione a sinistra, la sottrazione, e per ultima l’addizione: B = 3 + 1 = 4.

Calcoli con le parentesi

Se nell’espressione sono presenti le parentesi, si iniziano a risolvere i calcoli all’interno delle parentesi. Questi calcoli vanno sempre svolti rispettando le precedenze di cui si è parlato nella sezione 1.
Primo esempio: C = 9 – (3 x 2 + 1).
Si comincia calcolando 3 x 2 + 1, che si trova tra parentesi. In questo calcolo dobbiamo prima risolvere la moltiplicazione, che ha la precedenza:
C = 9 – (6 + 1).
Ottenuto il risultato all’interno delle parentesi, possiamo procedere:
C = 9 – 7 = 2.
Secondo esempio: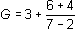
Tale espressione può essere scritta nella forma seguente:
G = 3 + (6 + 4) ÷ (7 – 2).
Si comincia dal calcolo di 6 + 4 e 7 – 2, che danno: G = 3 + 10 ÷ 5.
Poi possiamo effettuare la divisione, che ha la precedenza sull’addizione: G = 3 + 2 = 5.

Calcoli con numeri relativi

Come si calcola un’espressione in cui compaiono addizioni e sottrazioni di numeri relativi?

Calcolare una somma algebrica

In generale, il calcolo si esegue procedendo da sinistra verso destra.
Esempio: Per effettuare (-2) + (-1,5) – (-0,3), calcoliamo prima (-2) + (-1,5), poi sottraiamo (-0,3) al risultato ottenuto. Possiamo presentare i calcoli mostrando a ogni riga un singolo passaggio:
A = (-2) + (-1,5) – (-0,3)
A = (-3,5) – (-0,3)
A = (-3,5) + (+0,3)
A = -3,2

Risulta essere possibile modificare l’ordine dei termini per facilitare il calcolo.

Esempio: B = (-24,8) – (-32,5) + (+24,8)
B = (-24,8) + (+24,8) – (-32,5)
B = 0 + (+32,5)
B = +32,5

Scrittura semplificata di una somma algebrica

-Per i numeri positivi, la scrittura del segno + e delle parentesi è facoltativa.

-In una somma, se il primo termine è negativo, le parentesi che lo racchiudono sono facoltative.
-Addizionare un numero equivale a sottrarre il suo opposto (e sottrarre un numero equivale ad addizionare il suo opposto).

 Esempio con due termini

(+7) – (+2) si può scrivere 7 – 2 come ci dice la regola A.
Scriviamo: (+7) – (+2) = 7 – 2 = 5.
(-3) + (+1) si può scrivere (-3) + 1 come ci dice la regola A; poi -3 + 1 come ci dice la regola B.
Scriviamo: (-3) + (+1) = -3 + 1 = -2.
(+1) + (-4) si può scrivere (+1) – (+4) come ci dice la regola C; poi 1 – 4 come ci dice la regola A.
Scriviamo: (+1) + (-4) = 1 – 4 = -3.

Espressioni con più parentesi una dentro l’altra

Cominciamo effettuando i calcoli nelle parentesi più interne.
Esempi con due termini:
C = (-5) – ((-2) + (+7))
C = (-5) – (+5) = (-5) + (-5) = -10
D = [(-1,2) – (-2)] – [3 – (7,1 – (-8,5) + (-3)].
Utilizziamo le scritture semplificate:
D = [-1,2 + 2] – [3 – (7,1 + 8,5 – 3)]
D = 0,8 – [3 – 12,6]
D = 0,8 – [-9,6]
D = 0,8 + 9,6
D = 10,4

Articoli Simili