Come Calcolare le Diagonali di un Rettangolo

In questa guida spieghiamo come calcolare le diagonali di un rettangolo.

Iniziamo con il dire che con rettangolo si intende un quadrilatero caratterizzato da lati paralleli a due a due della stessa lunghezza e da angoli di 90 gradi. Vista la sua struttura, è dotato anche di due diagonali congruenti. Ognuna di queste divide la figura geometrica in due parti congruenti. Questo significa che le due parti hanno la stessa forma e la medesima area.

Stabilita la struttura del rettangolo, vediamo nel dettaglio come andare a calcolare le sue diagonali. Per portare a termine il procedimento ci si deve basare sul Teorema di Pitagora, secondo il quale in un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti. Questo teorema può essere applicato anche al caso del rettangolo, visto che viene diviso da ciascuna diagonale in due triangoli rettangoli congruenti.

Per spiegare meglio il calcolo delle diagonali di un rettangolo facciamo riferimento alla seguente figura.

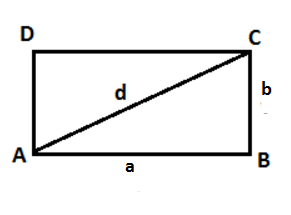
La base a e l’altezza b rappresentano i cateti del triangolo rettangolo che si è andato a formare, mentre la diagonale d è l’ipotenusa. Tutto questo per dimostrare che basta applicare, appunto, il teorema di Pitagora per ottenere questo tipo di formula.

$d^2 = a^2 + b^2$

Nello specifico, però, si deve calcolare d e non il suo quadrato. Per risolvere il tutto, dunque, si deve fare la radice quadrata di tutti e due i membri, ossia a e b.

$d = \sqrt{a^2 + b^2}$

Detto questo, dunque, la formula per trovare la diagonale di un rettangolo è

$Diagonale = \sqrt{base^2 + altezza^2}$

A questo punto, trovata la formula, vediamo come applicarla in concreto confrontandoci con un esempio. Supponiamo che, all’interno di un problema, ci si trovi a dovere ragionare su di un triangolo avente una base uguale a 15 cm ed una altezza pari a 28 cm. L’obiettivo è trovare la diagonale.

Tenendo sempre in considerazione il Teorema di Pitagora e quanto evidenziato fino a questo momento, possiamo dire che la soluzione del problema si articola sostanzialmente in quattro fasi. Il primo passo è rappresentato dalla necessità di elevare al quadrato la misura della base ottenendo questo risultato:

$15 ^2= 225$

Lo stesso tipo di calcolo, poi, deve essere fatto anche con l’altezza, arrivando a questo tipo di valore.

$28 ^2= 284$

Si è arrivati al terzo passaggio, rappresentato dalla somma tra i due valori ottenuti

225 + 784 = 1009

Per concludere, nel quarto e ultimo passo si deve trovare la radice quadrata della somma dei due numeri.

$\sqrt{1009} = 31,765$

La diagonale è quindi 31,765 nell’esempio proposto.

Articoli Simili